UFLDL: Sparse Coding

Sparse Coding

Sparse Coding 可以看做一种 unsupervised learning 的方法，作用是从数据里学习一组 over-complete 的 basis，使得输入数据 x 可以表示为这些 basis 的线性组合。 根据 UFLDL 的说法，这些 basis 可以反映、捕捉输入数据内在的一些规则与结构：

The advantage of having an over-complete basis is that our basis vectors are better able to capture structures and patterns inherent in the input data.

Over-complete 的作用相当于是增强冗余。假设我们使用 autoencoder 学习到了图像的 2 个 edge feature（想象成是横与竖），那么对于对角线这样的 edge，对应的 coeffifient 需要对这两个 feature 进行插值，一旦有 noise，就很容易造成 coefficient 的变化。 想对地，如果我们学到了，比如 64 个 edge，那么每个 edge 可以看做是互相的插值， 而对应的 coefficient 也比较 smooth：表示任意角度的 edge 我们都可以只需要给临近的几个 edge features 非零系数即可。根据 wiki 的说法，这与人类视网膜的结构类似：

The human primary visual cortex is estimated to be overcomplete by a factor of 500, so that, for example, a 14 x 14 patch of input (a 196-dimensional space) is coded by roughly 100,000 neurons.

Sparsity and Under-determined Linear system

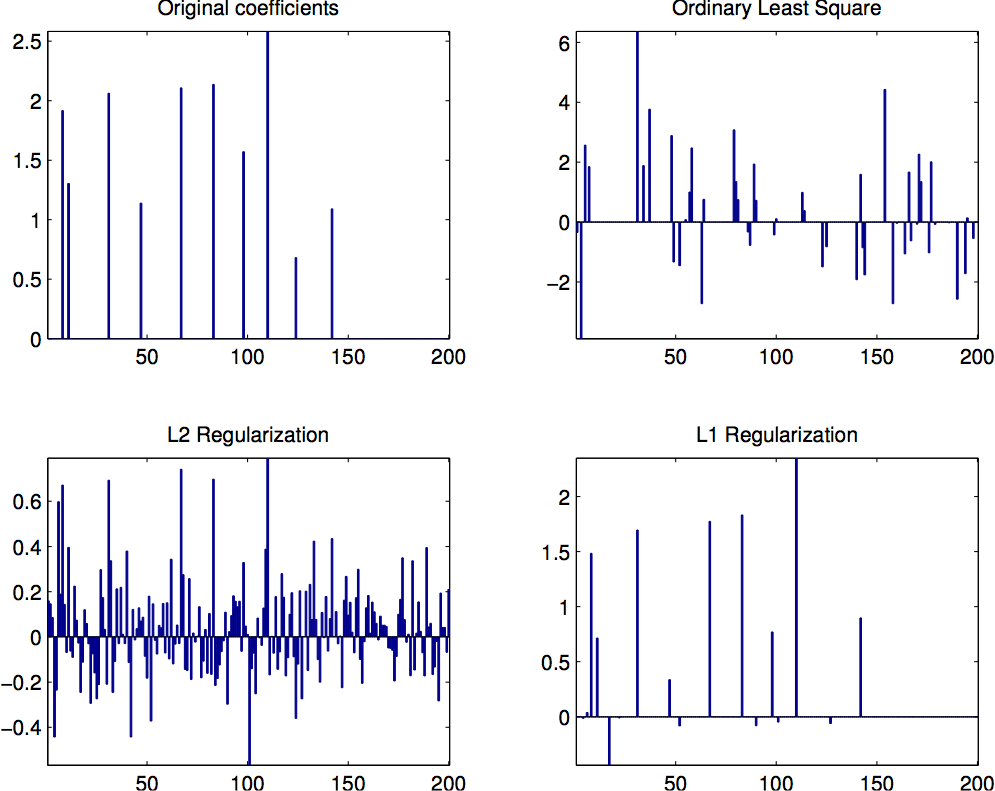
因为跟 “sparse” 有关，我首先从线性代数的角度阐述一下。

假设我们有数据 \(x \in R^n\), 那么每个维度 就是一个 basis。如果我们旋转这组数据，就相当于得到了另外一组 basis。一般来说， 如果数据维度是 n，那么我们就需要 n 个这样的 basis 来表示数据。如果我们把这些 basis 看做一个矩阵 \(A \in R^{n \times n}\)，其中每个 column 是一个 basis，\(s \in R^n\) 是数据在这个 basis 下的 coefficient，那么 \(x = As\)，就是相当于把数据映射到这个空间后的值。 显然，当 \(A\) 是方阵并且这些 basis 是 linear indeependent时，给定 x 后解 s 是唯一的。

但是当 A 的行数小于列数时，即 \(m < n\)，这时的 linear system 是 under-constrained, 那么会有无穷多个解。如下面的 matlab code 所示，我们用 \ (最小二乘法) 以及 pinv (伪逆矩阵) 求解得到的 s 是不同的。

但是如果我们加入了一些 constraint，情况就会有所不同。具体来说，我们希望 coefficient 里面的 non-zero elements 尽可能地说，也就是所谓的『sparsity』 constraint。

值得注意的是， PCA 也是找 basis 的一种方法， 但是 PCA 只能找到 \(k \le n\) 的 basis， 所以无法解决我们的问题（我们需要 \(k > n\)）。 对于 Sparse Coding Exercise 里用到的 20000 个 8x8 的 image patch，用 PCA 找到的 basis 看起来是这样的：

Sparse Coding: Objective Function

我们再考虑这个问题：假设 \(x\) 是输入数据，我们希望寻找到 k 个 basis \(\phi_i\) 使得 \(x\) 能被表示为他们的线性组合，其中 \(a_i\) 为对应的 coefficient，i.e.,

\[x = \sum_{i=1}^k a_i \phi_i\]

使用经典的 least square method，对于 m 个数据 \(D = \{x^{(1)}, \ldots, x^{(m)}\}\)， 我们可以写下如下的 Objective function 进行优化：

\[\min_{a_i^{(j)}, \phi_i} \sum_{j=1}^m \left\lVert x^{(j)} - \sum_{i=1}^k a_i^{(j)} \phi_i \right\rVert^2\]

注意到三点：

1. 不同于经典的 linear system, 这个 Objective function 我们有两样东西要优化： 系数 \(a_i^{(j)}\) 与 basis \(\phi_i\) (稍后解释[如何处理][Sparse Coding: Optimization])。
2. 这个 Objective function 的解可以有无穷多个（因为是 under-determined）。
3. 对于一组解，我们可以 scale up \(a_i^{(j)}\) 同时 scale down \(\phi_i\) 从而得到新的解， 但事实上这是冗余的。

如上面所讨论的，我们希望系数 \(a_i^{(j)}\) 是 sparse 的，也就是说，对于每个数据 \(x^{(j)}\), 我们希望尽可能多的 \(a_i^{(j)}\) 为 0。如果用 \(S(a)\) 来表示一个 penalize sparsity 的 function，当 \(\vert a\vert > 0\) 时，\(S(a)\) 返回一个很大的 cost。理论上，我们可以使用所谓的 \(L_0\) norm 作为这个 cost function，也就是当 \(a=0\) 时 \(S(a) = 0\), 否则 \(S(a) = 1\). 可是这个 function 既不是 smooth 也不不可微。所以我们一般使用 \(L_1\) penalty \(S(a) = \vert a\vert _1\) 或者 log penalty \(S(a) = \log (1+a^2_i)\). 为了解决第三个问题，我们可以限制 \(\phi_i\) 的 scale。把所有以上考虑进去，我们可以得到新的 Objective function:

\[\begin{split} \min_{a_i^{(j)}, \phi_i} & \sum_{j=1}^m \left\lVert x^{(j)} - \sum_{i=1}^k a_i^{(j)} \phi_i \right\rVert^2 + \lambda \sum_{i=1}^k S(a_i^{(j)}) \\\\ s.t. & \left\lVert \phi_i \right\rVert^2 \le C, \forall i=1, \ldots, k \end{split}\]

其中第一项可以看为 reconstruction cost, 第二项看为 sparsity penalty, \(\lambda\) 是 scaling factor，\(C\) 是一个常数。

Sparse Coding: Autoencoder Interpretation

以上的优化问题，其实可以看作一个 sparse autoencoder 的变种：input layer 对应于 sparse feature s, hidden layer 则是已知数据 x，他们之间的 connection 是 \(W^{(1)} = A\)，A 的每个 column 对应于一个 basis。我们希望学习到 A 与 s， 使得 x 能被 \(As\) 重构，因此 \(\vert As - x\vert _2^2\) 可以看做 reconstruction cost。 从线性代数的角度来说，A 可以看做一个 linear transform，s 是数据在 feature space 的 representation，而 x 是原始数据的 representation。As 的效果是把数据从 feature space 映射到 data space。 同时，我们希望 feature 是 sparse 的，因此我们有 sparsity penalty term \(\lambda \vert s\vert _1\)。这个 Objective 写为：

\[\begin{split} \min_{A, s} & \left\lVert As - x \right\rVert^2_2 + \lambda \left\lVert s \right\rVert_1 \\\\ s.t. & \ A^T_j A_j \le 1 \ \forall j \end{split}\]

其中 \(A^T_j A_j \le 1\) 是为了限制 basis 的 norm 大小而设置的，如上面所讨论。 注意到加了这个 constraint 后上面是一个 constrained programming problem， 要使用类似 gradient descent 的算法解决此类 问题，我们可以把 constraint 加到 Objective 里，成为一个所谓的 『weight decay』 term。因此我们定义 Objective function \(J(A,s)\) 为：

\[J(A, s) = \left\lVert As - x \right\rVert^2_2 + \lambda \left\lVert s \right\rVert_1 + \gamma \left\lVert A \right\rVert^2_2\]

注意到几点：

1. \(\min J(A, s)\) 此时是一个 unconstrained programming，并且主要有三个 term 组成， 分别是 reconstruction cost, sparsity penalty, weight decay term。
2. \(L_1\) norm 在 0 点时无法求导。一般的方法是用 approximation 的方法来 “smooth out”。 具体地， 我们使用 \(\sqrt{s^2 + \varepsilon}\) 来代替 \(\vert s\vert _1\)。其中 \(\varepsilon\) 是一个 smoothing parameter, 当 \(\varepsilon\) 比 \(s\) 大时， \(x+\varepsilon\) 会被 \(\varepsilon\) 所 dominate, 所以整个 sqrt term 会约等于常数 \(\sqrt{\varepsilon}\)。 换句话来说，当 \(s\) 足够小（符合 sparsity constraint），这个 approximation 的产生的最小 penalty 为 \(\varepsilon\)；否则， 这个 approximation 相当于 penalize non-sparsity。 因此 \(J(A, s)\) 可以改写为：

\[J(A, s) = \left\lVert As - x \right\rVert^2_2 + \lambda \sqrt{s^2 +\varepsilon} + \gamma \left\lVert A \right\rVert^2_2\]

其中 \(\sqrt{s^2+\varepsilon}\) 是 \(\sum_k \sqrt{s_k^2+\varepsilon}\) 的简写。

值得一提的是，从推导的过程中，我们可以看到，从最简单的 reconstruction cost 开始， 我们逐步地加入更多的 cost/penalty terms 来处理 constraints，包括 sparsity 以及 weight decay （regularization）。这其实在 convex optimization 里也是很常用的技巧： primal-dual。 对于原始的 constrained problem（primal），我们会定义一个 dual problem， 并且把 constraints 加到原来的 Objective function 里使得问题变成 unconstrained。这个 technique 叫做 lagrangian relaxation；加上去的这些 terms 对应的 coefficients 称为 lagrangian multipliers。Dual problem 里，原来要优化的变量我们看做常量， 而 lagrangian multipliers 是要优化的变量。 可以证明这个 dual problem 是 convex 的。在我们这个问题里， 我们并没有直接优化 dual problem，相反地，我们把 lagrangian multipliers 定义为常量， 可以理解为一种 heuristic，因为这些 multipliers 也是可调的参数。

此外，对于不可导的函数， 采用 approximation 的方法把他们替代为可导的函数也是很常用的技巧。 另外一种常见的 approximation 是把 \(max(x)\) 替代为 log-sum-exp (x)，因为 exp 会把 max(x) 放大，然后加起来取 log 相当于这个 max(x) 会 dominate 整个 function。

Sparse Coding: Topographic Features

个人觉得 UFLDL 上关于这一块讲得不是特别清楚，所以这里会把它尽量解释清楚。 并且加入了大量的例子以及 visualization。 根据上面所述，我们会学习到 basis A 以及 feature s。但是根据观察，人类大脑皮层检测 edge 方向的神经元往往是有序的。具体来说，相邻的神经元检查的 edge 朝向接近， 比如检查 40, 45, 50 度的神经元相邻的。所以，我们也希望学习到的 feature 是 topographically ordered。直观来说，这样的效果是，如果某个 feature i 的值非零， 那么相临的 i-1, i+1 等，也应该是相似的非零值。比如说 s 大概长成 [0.0 0.0 0.12 0.34 0.67 0.95 0.73 0.45 0.32 0.11 0.0 0.0] 这样子。

我们原来的 sparsity penalty 只要求 feature 有 sparse 特性。 对于每个 feature \(s_i\)，我们只有一个对应的 penalty term \(\sqrt{s_i^2 + \varepsilon}\)。 反映到 2D 图像上， 如果我们希望 impose topographic ordering，我们可以 “group” 相邻的 features，使得某个 feature activate 时，周围区域的 features 也该 similarly activate。所以如果把这个 feature vector plot 出来，看起来某个地方是有一个明显的块状。这意味着，比如 40 - 50 度的 neurons 会被 activate。如面两图所示，左右分别是 Topographic / Non-topographic Features 与 Basis。可以看到，topographic features 的图像里有很多明显的小方块，而 nontopographic 看起来只是一堆无规律的 noise。对于 Basis images 则更明显了， non-topographic basis 看起来正是使用 sparse autoencoder 学习到的 edge features。 而 topographic basis 则是很漂亮地排了序。

好了，有了 intuition，我们具体怎么做呢？假设我们把 feature vector 重新排成一个 square matrix，我们希望把 3x3 regions group 起来，那么我们只需要在 sparse penalty 里加入类似这样的项：

\[\sqrt{\sum_{i=1}^3 \sum_{j=1}^3 s_{i,j}^2 + \varepsilon}\]

其中 \(s_{i,j}\) 代表第 \(i\) 行 \(j\) 列的 feature。上面表示的是把 (1,1) - (3,3) 这个区域的 features group 起来。对于所有的 3x3 regions，我们都该加入类似的项， 可以想象成对这个 feature matrix 用一个 sliding window 生成所有项。

这里我们可能会有疑问：我们是对 feature 进行 grouping，为什么出来的 basis 就被『排序』了呢？直观来说，如果我们把每个 basis 看做一个 neuron，并且把它们排列成一个 matrix， 我们希望相邻的 neurons 能检测『接近』的 edges，所以每个小区域里的 neuron 对应的 edge filter 总是相似的（如上面左下图所示）。所以如果 features 的 value 总是成块出现的，对应的 neurons 也该被 “block activated”。具体到矩阵运算上面，参考下面的 1D 例子：

   A    * s = x             B    * t = x
1 0 0 0   1   1          1 0 0 0   1   1
0 1 0 0   1   1          0 0 1 0   0   1
0 0 1 0   0   0          0 0 0 1   1   0
0 0 0 1   0   0          0 1 0 0   0   0

其中 A 与 B 是 Basis matrix，每个 column 对应与一个 basis。注意它们是代表的 是完全相同的 basis space，只是 column 排列顺序不同。 并且，A*s 与 B*t 都生成相同的 x， 但 s 里的两个 non-zero 是相邻的，而 t 则非相邻。

至此，我们已经理解了如何进行 topographic sorting，因此，我们可以重写 Objective function 为：

\[J(A, s) = \left\lVert As - x \right\rVert^2_2 + \lambda \sum_{\text{all groups g}} \sqrt{\left( \sum_{\forall s \in g} s^2 \right) + \varepsilon} + \gamma \left\lVert A \right\rVert^2_2\]

我们可以只用一个 “grouping matrix” V 来方便程序实现，其中 V 的每行代表一个 group； \(V_{r,c}=1\) 代表 group \(r\) 包含 feature \(c\)。换句话说， V 是一个『选择』矩阵。 举例来说，假设我们把一个 feature vector \(s\in R^9\) 看成一个 3x3 matrix， 把 matrix 里的每个 2x2 region看做一个 group，那么就会有四个 group：1245, 2356, 4578, 5689. 下面的代码说明了如何使用 V 来实现 grouping （请把 [1 … 9] 看做 \(s_1^2, \ldots, s_9^2\)）：

 1 2 3 4 5 6 7 8 9
         V           s^2
 1 1 0 1 1 0 0 0 0   [1 2 3 4 5 6 7 8 9]^T   =>   1 + 2 + 4 + 5
 0 1 1 0 1 1 0 0 0                                2 + 3 + 5 + 6
 0 0 0 1 1 0 1 1 0                                4 + 5 + 7 + 8
 0 0 0 0 1 1 0 1 1                                5 + 6 + 8 + 9

因此，我们把 Objective function 改写为：

\[J(A, s) = \left\lVert As - x \right\rVert^2_2 + \lambda \sum \sqrt{V s^2 + \varepsilon} + \gamma \left\lVert A \right\rVert^2_2\]

其中 \(\sum \sqrt{V s^2 + \varepsilon} = \sum_r \sum_c D_{r, c}\), \(D = \sqrt{V s^2 + \varepsilon}\)

注意我们还应该实现 “wrapping around”，细节请参考 UFLDL。

Sparse Coding: Vectorization and Summary

以上的推导都是只假设了一个 sample x 以及一个 feature vector s。高效的实现时需要完成 vectorization。 如果我们用 \(S\) 以及 \(X\) 代表 feature 以及 data matrix， \(S^{(i)}\), \(X^{(i)}\) 对应于第 i 个 column，那么最终的 Objective 为：

\[J(A, S) = \frac{1}{m}\sum_{i=1}^m \left\lVert AS^{(i)} - X^{(i)} \right\rVert^2_2 + \lambda \sum \sqrt{V S^2 + \varepsilon} + \gamma \left\lVert A \right\rVert^2_2\]

注意这里的 \(S^2\) 是指 \(S \circ S\)¹。

在 matlab 里，我们可以 vectorize 上面一些步骤。比如 reconstruction cost 可以写成 sum(sum((A*S - X).^2)) / m。 其中里层的 sum 相当于算出每个 sample 的 reconstruction cost，即 \(\left\lVert As^{(i)} - x^{(i)} \right\rVert^2_2\)， 而外层的 sum 则是把所有的 cost 加起来。具体的 code 请参考我的 solution.

Sparse Coding: Gradients

上面提到，我们有两个变量需要优化：A, s。注意到，\(J(A, s)\) 里的 sparsity 以及 weight decay term 都是 convex 的。问题出在 reconstruction cost 上：它不是 convex 的。 根据 UFLDL ，以及 A. Ng nips06 的 paper [1]，观察到 fix A (或 s)， 则对于 s （或 A），\(\left\lVert As - x \right\rVert^2_2\) 都是 convex 的。 因此，我们可以迭代解决对于 A 与 s 的优化问题。直观来说，这有点像 [EM] 算法： 每次固定一个变量时，我们都能得到另外一个变量的新的、更小的 upperbound。如此迭代下去， 每个变量都能保证至少不比上一次迭代要大，直到收敛。

对于 \(\min_A J(A ; s)\) （注意符号，读作 find A that minimizes J(A, s) given s）， 我们可以 drop 掉 sparse penalty （因为与 A 无关），\(J(A; S)\) 只是一个关于 A 的 quadratic optimization，所以我们可以很容易得到一个 closed-form formula，只需要 使关于 A 的 gradient 为零，也就是：

\[\nabla_A J = 0 \Leftrightarrow 2 (As - x) s^T + 2 \gamma A = 0 \Leftrightarrow A = xs^T (s s^T + \gamma I)^{-1}\]

其中关于 \(\left\lVert As - x \right\rVert^2_2\) 的 gradient 计算请参考 The matrix cookbook 公式 (83)。注意上式针对的是 s, x 为 vector 的情况。我们现在来考虑 \(J(A; S)\)。注意到我们可以用 Frobenius norm 的形式来表示 \(J(A, S)\):

\[J(A, S) = \frac{1}{m} \left\lVert AS - X \right\rVert^2_F + \lambda \sum \sqrt{V S^2 + \varepsilon} + \gamma \left\lVert A \right\rVert^2_2\]

其中 \(\left\lVert A \right\rVert^2_F = \sqrt{\sum_i \sum_j \left \vert a_{ij}\right \vert ^2}\)，所以我们有：

\[\nabla_A J = 0 \Leftrightarrow 2 (AS - X) S^T / m + 2 \gamma A = 0 \Leftrightarrow A = XS^T (S S^T + \gamma m I)^{-1}\]

可以看到，与 vector 形式是很相似的。

对于给定 A 求 S 的情况，很遗憾我们无法找到一个 closed-form formula，因此我们尝试使用 gradient descent。首先我们要找 S 的 gradient，难点在 sparsity penalty term \(\lambda \sum \sqrt{V S^2 + \varepsilon}\) 里，注意这里有点滥用数学符号： \(\sqrt{\cdot}\) 与 \((\cdot)^2\) 在这里都是指 element-wise 的运算。 这里似乎使用最原始的方法展开整个表达式来推导 gradient 比较直观，或者把式子当做 复合函数然后使用 chain rule 来进行求导， 我暂时没有想到很简洁的矩阵表达方法。这里给出最后的 gradient 为：

\[\nabla_S J = V^T (V S^2 + \varepsilon)^{(-1/2)} \circ S\]

Sparse Coding: Optimization

如上面所提到的，因为整个问题是 non-convex 的，我们必须迭代求解 \(A\) 与 \(S\) 进行优化。 然而正如 EM 等算法，我们必须先解决先有鸡还是先有蛋的问题：假设我们先优化 \(A\)，则必须 先有一个 \(S\) 的初始值。根据 UFLDL， 随机产生的 \(S\) 很可能使得优化收敛速度过慢。 一个好的初始化 \(S\) 的方法如下:

• \[S \gets A^T X\]
• 对于每个 \(s = S^{(i)}\)，使用对应的 basis \(A^{(i)}\) 进行 normalize。也就是：

\[s \leftarrow \frac{s}{\norm{A^{(i)}}}\]

此外，一个实际的考虑是如果我们每轮迭代都使用所有的数据进行优化，也就是所谓的 batch 方法，那么优化时间会过长。想对地，如果我们每次使用一个随机的子集，比如 2000 out of 10000， 来进行优化，往往优化速度可以被大大加快。

Experimental Results and Observations

以下是我在完成 Sparse Coding Exercise 时的一些观察与体会：

• 大量参考了这里。 证实了里面提到的两点：
  1. normalize 会产生问题。表现为每个 Iteration 的 fObj 震荡很厉害（e.g., 12.34, 623.12, 10.12, 702.12, …）。
  2. 在优化算法层面上 lbfgs 似乎的确不如 cg 得到的结果好。根据观测， lbfgs 收敛快并且能跳出 local minimum，最后得到的结果看起来不如 cg 好，但是跟初始解不一样。 而 cg 更稳定，做成动画 (youtube, tudou) 后，能看出基本上 feature 的 topographic 跟初始解差不多，但是慢慢地会 learn 到一些更清晰的 edges。
• UFLDL Sparse Coding Exercise 里的 \(s s^T\) 应该是 \(s^2\) 或者 \(diag(s s^T)\)，因为 s 是 column vector，而我们要生成 \(s \circ s\) (element-wise square, dot product)。
• 关于使用 backpropagation 算法来推导 gradient，UFLDL 上的推导似乎不是很严谨。在 Example 2 里推导 A 时，A 是作为第一层的 weight 存在，即 \(W^{(1)}\)。 如果严格按照 BP 算法，那么对于 \(A=\nabla W^{(1)}\) 应该只需要计算到第二层的误差 \(\delta\)，使得 \(\nabla W^{(1)} = \delta^{(2)} (a^{(1)})^T\)。而教程里是直接算到了第一层的误差 \(\delta^{(1)}\). 而在 Example 3 里推导 s 时，s 却是作为输入存在的（第一层的 neurons），同样也需要算到第一层的误差，同时，经典 BP 里的 gradient 算的总是针对 connections 上的 weight，而这里 s 是 input layer。 一个 unified 的办法也许是加多一个第 0 层，输入是 \(I\) (Identify function)，并且把 \(W^{(0)}\) 设置为需要计算 gradient 的矩阵（也就是说， Example 2 里是 A, Example 3 里是 s），连接到第 1 层上。那么这时算我们要算的 gradient 就统一为 \(\nabla W^{(0)}\) 了。

References

1. [1]H. Lee, A. Battle, R. Raina, and A. Y. Ng, “Efficient sparse coding algorithms,” in Advances in neural information processing systems, 2007, pp. 801–808.

1. Element-wise multiplication. See more details here. ↩